


|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
INDIAN VERSUS WESTERN MUSICBy Ketil Helmersberg At the heart of Indian music is the raga, which is a mood, a sentiment, expressed by a microtonal scale. There are many different ragas, and each has its own mood and its own corresponding microtonal scale based on what is called the natural harmonic series - the natural law of vibrations. However, in the latter 100 years or so, Indian music has been influenced by a foreign tonal system that is not based on the natural harmonic series. This is the Western tonal system, which has influenced Indian music mainly by Indian musicians adopting fixed-pitch Western instruments. Especially, this is the case with the harmonium, which has become very popular and widespread in India. The tonal system of Western music is based on an artificial division of the octave into twelve equal intervals. This means first of all that the notes actually are out of tune, but also that the number of intervals available for musical expression are very limited, as compared to the infinite possibilities of the natural harmonic series. Hence, it is not possible to play a raga properly using a fixed-pitch instrument based on the Western tonal system. It is like trying to make a copy of a painting without having access to the correct colors of the original. It is a system that is incapable of expressing all the subtle nuances of the natural intervals employed in the large number of ragas. The Western tonal system has, however, become so dominant in the world today, as also in India, that the original microtonal scales of the ragas are in danger of getting lost. Many scholars of Indian music consider this development to be very unfortunate, not only for Indian music as an art form, but first of all because the ragas originally are meant to be a means for development of consciounsess. By replacing the original microtonal scales with approximations of Western scales, the original strength and power of the ragas are getting lost - which is not only a theoretical consideration, but first of all based on experience. Because of this, we believe it important to raise awareness of this issue. We therefore give in the following a description, a comparison and a historical resume of the original Indian and Western tonal systems. THE ESSENCE OF MUSICThe essence of music can be said to be relationships of sounds. If we look up the word "music" in the Oxford dictionary, it gives the following definition: Definition of music according to Oxford dictionary
Vocal or instrumental sounds (or both) combined in such a way as The sounds of music are both in traditional Western and Indian music ordered in scales, which thus are the basis for musical expression. Most commonly a scale has 7 notes, while it sometimes can have less and sometimes more. One of the notes of the scale is called the key note, the basic note of the scale. If you can liken it to a family, the key note is like the mother, while the rest of the notes are like the children. Sometimes the children are playing between themselves, but always with the mother in the background and always returning to the mother. Hence, the most important relationships between the notes of a scale are between each of the notes and the key note. The key note is the starting note from which we build a music scale. The different notes of a scale are often named by their position from the key note. Hence, the second note of a scale is called the second, the fourth note the fourth, the fifth note the fifth, and so on. INTERVALS OF JUST INTONATIONWhen we strike a string on a guitar, it makes a sound. The sound comes about by the vibrating string making the adjacent molecules of air vibrate. The vibration spreads in all directions in space, like ripples in a pond. When it reaches our ear membranes, it makes them vibrate, and this is then transformed into nerve impulses that we perceive as a continuous sound of a definite pitch. The air vibrate in the same speed as the string, and the pitch of the sound is determined by the speed of the vibration, which is called the frequency. The frequency is measured in Hz, which is the number of vibrations pr. second. The frequency of the vibrating string is determined by its length, thickness and tightness. Disregarding possible amplification devices, the amplitude of the vibration determines the volume. While the frequency, and thus the pitch of the sound, stays the same as long as the string is vibrating, the amplitude gradually diminishes, making the sound slowly fade away. When we listen to the sound of a guitar string, we do not only hear one sound, but many sounds of different pitch. We actually hear a compound of sounds. We hear one sound that is most prominent, the basic sound, but in addition so called overtones. The intervals, which are the differences in pitch, between these sounds, are not at random, but very precise and orderly. Disregarding possible limitations of the physical medium of the string, the overtones are exact multiplications of the frequency of the basic sound. If for instance the main sound is 200 Hz, the first overtone, which is the second sound, will be 400 Hz, twice the basic frequency. The second overtone, or the third sound, will be 600 Hz, three times the basic frequency. The third overtone, or the fourth sound, will be 800 Hz, four times the basic frequency. The fourth overtone, or the fifth sound, will be 1000Hz, five times the basic frequency, and so on. We can illustrate this by using a scale of frequencies in Hz: A sound and its overtones 
This sequence of sounds is called the harmonic series and represents a collection of natural intervals. They embody the sound intervals of nature, also called intervals of just intonation. In the most prominent cultures of the world's history, one built one's musical scales on such intervals. Also in Europe - all through the middle ages and in the renaissance - there was a general agreement that intervals of just intonation should be the basis for music. The intervals of just intonation can be expressed as ratios of the sound numbers of the harmonic series, which are one number divided by the other. We can illustrate this in the following way: Mathematics of Just Intonation 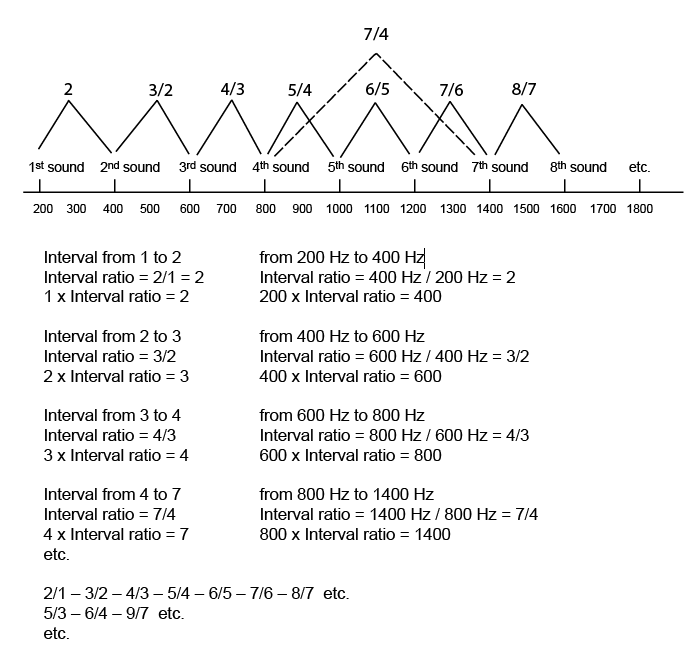
The interval ratio between two sounds in the harmonic series is the number of the last sound divided by the number of the first sound. By multiplying the number of the first sound with the ratio one gets the number of the last sound. The following demonstrates this: The first interval we have is from sound 1 to sound 2, which in this case is from 200 Hz to 400 Hz. This is also called an octave. The ratio for this interval is 2/1. By multiplying 1 with the interval ratio, we get 2. Likewise, by multiplying 200 Hz with the interval ratio we get 400 Hz, the frequency of the 2. sound. The second interval we have is from sound 2 to sound 3, which in this case is from 400 Hz to 600 Hz. The ratio for this interval is 3/2. By multiplying 2 with the interval ratio, we get 3. Likewise, by multiplying 400 Hz with the interval ratio we get 600 Hz, the frequency of the 3. sound. The third interval we have is from sound 3 to sound 4, which in this case is from 600 Hz to 800 Hz. The ratio for this interval is 4/3. By multiplying 3 with the interval ratio, we get 4. Likewise, by multiplying 600 Hz with the interval ratio we get 800 Hz, the frequency of the 4. sound. But we also have intervals comprising more than one interval, like for instance from sound 4 to 7, which in this case is from 800 Hz to 1400 Hz. The ratio for this interval is 7/4. By multiplying 4 with the interval ratio, we get 7. Likewise, by multiplying 800 Hz with the interval ratio we get 1400 Hz, the frequency of the 7. sound, and so on. From the harmonic series can be found intervals of all sizes and degrees. An interval, or the difference between two intervals, can be so small that it is hardly detectable for an untrained ear. Such a minute difference is called a microtone, and scales based on the harmonic series are therefore called microtonal. We can also see that there is a mathematical principal involved. All the interval ratios in the harmonic series are expressed by whole numbers. So what characterizes natural intervals, or intervals of just intonation, is that they can be expressed as whole number ratios. This was also the discovery of the old Greeks, like Pythagoras, the Sumerians, the old Indians, the Chinese and many other cultures of the world history, who all thought that musical scales should be based on such intervals. Thus, one can choose a key note and build a natural scale, or a scale in just intonation, by adding intervals of whole number ratios. Which intervals to choose for a scale is a science by itself. In the Indian tradition the selection of intervals for a scale is such that playing the notes creates a specific mood or sentiment, which is called a raga. A basic principle is also that interval ratios of smaller numbers are more harmonious, or consonant, than those of larger numbers. As the numbers of the ratios become larger, the intervals become less consonant and more dissonant. By applying whole number ratios, one can make a collection of intervals within an octave, from the smallest to gradually larger. These intervals then constitute a series of notes from which one can select the ones to be used in a scale. In the European tradition, one has since long back used a tonal system with twelve intervals in the octave, constituting a series of notes called half tones. From these one selects the ones to be used in different scales. Originally, these twelve notes of western music were in accordance with just intonation. As an example, we can choose to give preference to the most consonant intervals, which have ratios of the smallest numbers, and make a collection of twelve somewhat evenly spread out notes within an octave. Thus, we will have a series of half tones in just intonation. We can start with the standard A in western music, which has the frequency of 440 Hz. Example of a series of notes in just intonation
As we see from the table, one can also calculate the interval ratios between the half tones. To do this, one takes the interval ratio for a note - calculated from the key note - and subtracts the interval ratio of the previous note - also calculated from the key note. This is done by an interval ratio being multiplied by the inverse of the interval ratio to be subtracted. For instance, to find the interval ratio from A# to B, one subtracts the interval ratio 16/15 from the interval ratio 9/8, which is done by the following multiplication: 9/8 x 15/16 = 135/128. One can also add interval ratios. To do this, one multiplies one ratio with the other. For instance to add the ratio 16/15, which is the half note from A to A#, to the ratio 135/128, which is the half note from A# to B, one do the following calculation: 16/15 x 135/128 = 9/8. From this series of twelve notes, one mostly uses 7 notes for a music scale - which normally would be a sequence of whole and half tones. However, when we calculate the interval ratios between the half tones in the twelve note series, we find that they are not equal. While the ratio from A to A# is 16/15, the ratio from A# to B is 135/128 etc. This means that if one should want to use another note than A as the key note, the sequence of intervals would not be the same. What this means in practice, is that to apply just intonation to a so called fixed-pitch instrument, like an organ or a piano, one has to tune the instrument in accordance with one specific key note. If one should want to change the key note, which means to start the same scale from another note, another pitch, one most likely would have to retune the whole instrument. This became a practical problem in Western music when one started to use fixed-pitch instruments, because one wanted to be able to frequently switch key notes, even in the middle of a composition. We can illustrate this problem by the following example: The twelve note series above is based on the key note of A. So if we use this to make an A-major scale, we will see what will happen if we for instance try to change the key note to C. The A-major scale consists of the notes A - B - C# - D - E - F# - G#, while the C-major scale has the notes C - D - E - F - G - A - B. An A-major scale in just intonation changed to a scale in C-major
What we see is that the intervals between the notes of the two scales in many cases become different. For instance, the interval between the first and second note of the A-major scale, from A to B, has the ratio 9/8, while the interval between the first and second note of the C scale, from C to D, has the ratio 10/9. The interval ratio between the second and third note of the A-major scale is 10/9, while the interval ratio between the second and third note of the C scale is 135/128, and so on. Because the intervals of the notes of these two scales in many cases are different, they are actually two different scales. It is therefore not possible to change the key note of the major scale from A to C with this sequence of intervals. THE TWELVE-TONE EQUAL
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Notes | Frequency equal temperament |
Frequency Just Intonation |
Frequency difference |
Ratio from Previous note | ||
| Equal | Just | |||||
| 1st | A | 440.0000 Hz | 440.0000 Hz | 0.0000 Hz | ||
| 2nd | A# | 466.1624 Hz | 469.3333 Hz | -3.1709 Hz | 1.05946 | 1.0667 |
| 2nd | B | 493.8824 Hz | 495.0000 Hz | -1.1176 Hz | 1.05946 | 1.0547 |
| 3rd | C | 523.2524 Hz | 528.0000 Hz | -4.7476 Hz | 1.05946 | 1.0667 |
| 3rd | C# | 550.0000 Hz | 554.3648 Hz | +4.3648 Hz | 1.05946 | 1.0417 |
| 4th | D | 587.3296 Hz | 586.6667 Hz | +0.6629 Hz | 1.05946 | 1.0667 |
| 4th | D# | 622.2524 Hz | 616.0000 Hz | +6.2524 Hz | 1.05946 | 1.0500 |
| 5th | E | 659.2564 Hz | 660.0000 Hz | -0.7436 Hz | 1.05946 | 1.0714 |
| 6th | F | 698.4560 Hz | 704.0000 Hz | -5.5440 Hz | 1.05946 | 1.0667 |
| 6th | F# | 739.9876 Hz | 733.3333 Hz | +6.6543 Hz | 1.05946 | 1.0417 |
| 7th | G | 783.9920 Hz | 770.0000 Hz | +13.9920 Hz | 1.05946 | 1.0500 |
| 7th | G# | 830.6100 Hz | 825.0000 Hz | +5.6100 Hz | 1.05946 | 1.0714 |
| Oct. | A | 880.0000 Hz | 880.0000 Hz | 0.0000 Hz | 1.05946 | 1.0667 |
As seen from the table, the differences in frequency between equal temperament and just intonation might seem small in numbers. The supporters of the twelve-tone equal temperament system will therefore probably claim that this difference is not of great importance. They also might ask why the intervals of just intonation should be more preferable, even if they can be considered to be so called natural, which means in accordance with the natural harmonics.
To answer this question, we will first consider the limitations of the twelve-note equal temperament system, and then its influence on the mind of the listener as compared to just intonation.
LIMITATIONS OF THE TWELVE-TONE
EQUAL TEMPERAMENT SYSTEM
The twelve-tone equal temperament system has great limitations for musical expression. While in just intonation, one has an infinite number of natural intervals available, one has in the twelve-tone equal temperament system only 12 fixed intervals accessible.
To illustrate this limitation, much of the world's folk music and contemporary music would not have existed in the form we know it if one only had to stick to the tempered scales. This concerns genres of music like Irish and English folk music, Negro Spirituals, Blues, Soul, many types of Jazz and Rock and Roll. The reason is that these genres of music rely heavily on intervals that not even approximately are available in the tempered system, as for instance the so called blue notes, which often are a lowered third, fifth or seventh of a scale, but not lowered as much as to reach the next half note of the equal temperament. These particular notes are in many ways the life-blood of these genres of music. Without them, they would loose their vitality and power of enchantment.
It is possible to create a kind of illusion of a blue note on for instance a piano by playing very fast intervals of half notes, and thereby create a feeling of a blue note, which is situated somewhere between two half notes. Hence, some pianists can to a certain degree compensate the limitations of the tempered system by their technical ability. But this is definitely not the same as playing the blue note itself, which is not available on an equal tempered piano.
The limitations of the tempered system are even more apparent when it comes to Indian music. There exists about 150 microtonal scales, or ragas, in India today, and they apply quite many more intervals than the number of twelve in equal temperament.
Concerning fixed-pitch instruments, there is also another limitation: An important feature to express a raga is to slide between notes of the scale. This is not possible on a fixed-pitch instrument like a piano or a harmonium, which therefore makes them less suitable for playing Indian classical music as a solo instrument, even if they should be tuned correctly.
Moreover, a limitation of the equal temperament is also that each note is fixed to a certain frequency. In traditional Indian music one never did that. Every frequency of sound has a particular influence, a particular quality or feel to it. If there weren't different feelings connected to different sound frequencies, there would, for instance, be no point of playing in different keys. By the fixity of the frequencies of the notes, the twelve tone equal temperament excludes many frequencies - obliterate them from nature's palette. If you liken the sound frequencies to the spectrum of colors, it is as if artists only had a small limited number of set colors to work with.
An essential consideration regarding intervals of sound is how they affect the mind. In classical texts of Indian music, as also in the Greek philosophy of Pythagoras and Plato, a key factor for music to have a positive effect is that it should be pleasing to the mind. Studies show that when people hear intervals of just intonation, they find them to be more pleasing, more beautiful than the equivalent intervals in equal temperament. People are actually often amazed that the intervals of equal temperament at all can be considered consonant, or harmonious, when hearing them after having heard the equivalent intervals in just intonation.
Esthetic reasons were also the main argument against the equal temperament when it was introduced in Europe. Musical theorists of the time felt that equal temperament degraded the purity of each chord and the esthetic appeal of music.
It is also interesting to note that none of the renowned western, classical composers wrote for equal temperament, including Bach, Mozart, Beethoven, Schubert, Schumann, Chopin, Liszt, Wagner, Brahms and Chaikovskii. Mozart is even quoted to have said that he would kill anyone that would play his music in equal temperament.
However, considering that the differences in frequency between the notes in equal temperament and the equivalent notes in just intonation are not very large, as seen in terms of percentages, why should there be such a difference in the pleasantness of hearing their intervals? Can it be just a question of imagination? Or some kind of a placebo effect?
The answer to this is that the intervals of just intonation are more consonant, or harmonious, than the equivalent intervals in equal temperament, which also can be shown by modern scientific experiments.
Consonance is a word derived from Latin: com, "with" + sonare, "sound." If we look it up in the Wikipedia, it will be defined as following:
Consonance
A harmony, chord or interval that are considered stable, as opposed to dissonance, which is considered unstable.
Dissonance is also a word derived from Latin: dis, "apart" + sonare, "to sound." It is defined by the modern musicologist Roger Kamien in the following way:
Dissonance
An unstable tone combination is a dissonance; its tension demands an onward motion to a stable chord. Thus dissonant chords are 'active'; traditionally they have been considered harsh and have expressed pain, grief, and conflict."
Both consonance and dissonance are important for musical expression, but it has a value that the consonant intervals are truly consonant. To show by modern scientific experiments that the intervals of just intonation are more consonant than the equivalent intervals in equal temperament, we have to go into a branch of physics called acoustics. This is a comprehensive science, because many features are involved in the relationship between sounds. We will therefore only look at what is considered to be the most important factor for consonance and dissonance, which is a phenomena called beating.
BEATING
When the difference in frequency between two sounds is more than zero Hz and less than about 20 Hz, we will perceive them as one sound. The frequency of the combined sound that we hear, will be the average of the two sounds. The volume of the combined sound, however, will for certain reasons constantly vary, and this is what is called beating. It is a phenomena that is considered to be the principal cause of dissonance. The reason why beating occurs is because of the constantly changing relationship between the vibrations of the two sounds.
When we strike a string on a guitar, the air molecules surrounding it starts to vibrate back and forth. The vibration spreads in all directions of space. The volume of the sound is an outcome of the amplitude of the vibration.
When the frequency of two sounds are so close together that they are perceived as one sound, the amplitude of the combined sound is the summation of the amplitudes of the two sounds. As one of the two sounds vibrates slightly faster than the other, the relationship between their vibrations will continuously vary. At one point they will be synchronous, which means that they will swing back and forth simultaneously and the sum of their amplitudes will be the maximum. Then they gradually will be less synchronous, which also means that the sum of the amplitudes gradually will be less, until they reach a point when they vibrate opposite each other. If they then have the same amplitude, the sum of their amplitudes will be zero, making no sound. If the amplitude of one of the two sounds is larger than the other, the amplitude of the combined sound will not be zero, but less than the sound with the largest amplitude. Then gradually the vibrations of the two sounds will move back to being synchronous, which also means that the amplitude of the combined sound gradually will increase until they again reach their maximum, and so on.
The sound that we hear is the result of the two sounds working against our ear membranes. When their vibrations are synchronous, they will push and pull the ear membranes simultaneously, and thus with a combined force stronger than one of them alone. Then when their vibrations are opposite each other, one sound will push the membranes, while the other will pull it, and thus they will more or less block each other, making us perceive a reduced sound, or no sound at all. This is what is called beating. It can be likened to listening to the radio while turning the volume rapidly up and down. The frequency of the beating is the difference in frequency between the two sounds. We can illustrate the phenomena by the following figure, which shows the sound vibrations as waves:
Example of beating
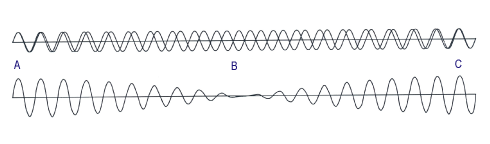
The two upper waves are the sounds, while the wave under is the combined sound that we hear. The two sounds have the same amplitude. The changing amplitude of the lower wave shows the change in volume of the combined sound. At point A the two sounds are somewhat synchronous, and the combined amplitude is at its largest. Then they become less synchronous and the combined amplitude becomes less. At point B they vibrate opposite each other and the combined amplitude becomes zero, making no sound. Then they gradually move back to synchrony, while the combined amplitude gradually increases and reaches its maximum when the two waves again become synchronous, and so on.
When the difference in frequency increases between two sounds, while still being less than about 20 Hz, the frequency of the beating increases. When the difference between the sounds becomes larger than about 20 Hz, the beating is replaced by an experience of roughness. When the difference reaches a point somewhere between a whole note and a minor third, the beating stops and we hear two separate sounds.
The phenomena of beating denotes that just a slight variance in frequency have a strong impact on the degree of consonance or dissonance. We can illustrate this by a mistuned interval of an octave:
Example of beating for a slightly mistuned octave
| Key note | Octave | Mistuned octave |
Beating between sounds |
||
| O v e r t o n e s |
10. sound | 4000 Hz | 8000 Hz | 8020 Hz | 10. - 5. = 10 Hz |
| 9. sound | 3600 Hz | 7200 Hz | 7218 Hz | ||
| 8. sound | 3200 Hz | 6400 Hz | 6416 Hz | 8. - 4. = 8 Hz | |
| 7. sound | 2800 Hz | 5600 Hz | 5614 Hz | ||
| 6. sound | 2400 Hz | 4800 Hz | 4812 Hz | 6. - 3. = 6 Hz | |
| 5. sound | 2000 Hz | 4000 Hz | 4010 Hz | ||
| 4. sound | 1600 Hz | 3200 Hz | 3208 Hz | 4. - 2. = 4 Hz | |
| 3. sound | 1200 Hz | 2400 Hz | 2406 Hz | ||
| 2. sound | 800 Hz | 1600 Hz | 1604 Hz | 2. - 1. = 2 Hz | |
| 1. sound | 400 Hz | 800 Hz | 802 Hz |
We see that between the key note and the pure octave, the overtones are in concurrence with each other on different levels, which means that there are no beating and that the two sounds therefore have a high degree of consonance. If we however mistune the octave by 2 Hz, we get beating between the overtones on many levels, between the 2nd and 1st sound, between the 4th and 2nd sound, between the 6th and 3rd sound etc. This will result in reduced consonance, or increased dissonance.
We can now compare the consonance of just intonation with that of equal temperament by using a pure fifth as an example. The fifth with the ratio of 3/2 is considered to be a highly consonant interval.
The comparative consonance of a pure fifth
in just intonation and in equal temperament
| Key note | Fifth 3/2 in Just Intonation |
Fifth tempered | Beating | ||
| O v e r t o n e s |
10. sound | 4400 Hz | 5940 Hz | 5931 Hz | |
| 9. sound | 3960 Hz | 5400 Hz | 5391 Hz | 9. - 6. = 6 Hz | |
| 8. sound | 3520 Hz | 5280 Hz | 5272 Hz | ||
| 7. sound | 3080 Hz | 4620 Hz | 4613 Hz | ||
| 6. sound | 2640 Hz | 3960 Hz | 3954 Hz | 6. - 4. = 4 Hz | |
| 5. sound | 2200 Hz | 3300 Hz | 3295 Hz | ||
| 4. sound | 1760 Hz | 2640 Hz | 2636 Hz | ||
| 3. sound | 1320 Hz | 1800 Hz | 1977 Hz | 3. - 2. = 2 Hz | |
| 2. sound | 880 Hz | 1320 Hz | 1318 Hz | ||
| 1. sound | 440 Hz | 660 Hz | 659 Hz |
The tempered fifth is actually 659.2564 Hz.
We see in this table that there are a large degree of concurrence between the overtones of the key note and the fifth in just intonation. By none of the sounds are there such a difference that beating can occur.
But if we look at the tempered fifth, none of the overtones are concurrent with the overtones of the key note, and we get beating between many of the overtones. We get beating between the 3rd and the 2nd sound, between the 6th and the 4th sound, between the 9th and the 6th sound etc. This means that the consonance is much weaker, or the dissonance much stronger, compared to the equivalent interval in just intonation.
JUST INTONATION IN COMBINATION
WITH EQUAL TEMPERAMENT
Still, someone might assert that even though a fixed-pitch instrument, like the piano or the harmonium, tuned in equal temperament, have their limitations, and that their intervals are less pleasing, why should it not be okay to use it for accompaniment for one who is singing or playing in just intonation?
To answer this question, let us first consider the singing by itself. In the Indian classical tradition of music, one is trained by ear to sing in just intonation. Studies also show that people in general, singing alone or in a vocal group, naturally tend to sing in just intonation when not being accompanied by a fixed-pitch equal tempered instrument. But what happens if you try to sing in just intonation when accompanied by an instrument tuned in equal temperament? Let's say one is singing in the A-major scale based on the intervals of just intonation shown above. And let's say that one sings a pure fifth, which in this case is the note E, while an A-major chord is being played on the instrument, which have the notes A - C# - E. Let's look at the following table to see how this will work:
A fifth in just intonation combined
with a fifth in equal temperament
| Key note A |
Fifth tempered E |
Fifth Just Intonation E |
Beating between the fifths |
||
| O v e r t o n e s |
10. sound | 3900 Hz | 6590 Hz | 6600 Hz | 10 Hz |
| 9. sound | 3520 Hz | 5931 Hz | 5940 Hz | 9 Hz | |
| 8. sound | 3200 Hz | 5272 Hz | 5280 Hz | 8 Hz | |
| 7. sound | 3080 Hz | 4613 Hz | 4620 Hz | 7 Hz | |
| 6. sound | 2640 Hz | 3954 Hz | 3960 Hz | 6 Hz | |
| 5. sound | 2200 Hz | 3295 Hz | 3300 Hz | 5 Hz | |
| 4. sound | 1760 Hz | 2636 Hz | 2640 Hz | 4 Hz | |
| 3. sound | 1320 Hz | 1977 Hz | 1980 Hz | 3 Hz | |
| 2. sound | 880 Hz | 1318 Hz | 1320 Hz | 2 Hz | |
| 1. sound | 440 Hz | 659 Hz | 660 Hz | 1 Hz |
The tempered fifth is actually 659.2564 Hz.
The piano or harmonium will play the key note and the tempered fifth, which is the notes A and E, while the singer will try to sing the note E in just intonation. If we then look at the difference in frequency between these two E notes, we see that not only are neither of their sounds concurrent with each other, but that we will get beating on all levels, both between the basic sounds and all the nearest overtones. This will probably create a very strong degree of dissonance, which most likely will force the singer to sing in equal temperament. Hence, to sing in just intonation while being accompanied by for instance an equal tempered harmonium will probably not be possible.
What these examples taken from the science of acoustics show is that very minute modifications of natural intervals, which in isolation might seem as trifles, might have far reaching distorting consequences on many levels.
CONCLUSION
To conclude. Western musicology has marred the harmony and beauty of the sound intervals of music by distorting their natural relationships. In addition, it has made a prison for its music by locking it out from a vast universe of potential musical expressions. It has even conditioned musicians to hear music that are in accordance with natural harmonics as being out of tune.
By incorporating fixed-pitch Western instruments into Indian music, the original strength and purity of this music is distorted and polluted. One is bringing the music away from the harmony of the laws of nature, while it is meant to do the opposite, to bring us more in tune with the laws of nature. We therefore believe it important to raise the awareness of this issue.